Intermodulation Measurement¶
Intermodulation AFM (ImAFM™) would not be possible without Multifrequency Lockin Amplifier (MLA™) also known as the Intermodulation Lockin Analyzer (ImLA™) [Tholen-2011]. The instrument is specially designed to make a phase-sensitive measurement of many intermodulation products generated by a nonlinear system that is driven by two or more tones.
Intermodulation should not occur when the cantilever is oscillating in air above a surface because the freely oscillating cantilever is a linear system. When the cantilever is oscillating close to a surface and the tip is interacting with the surface the cantilever oscillation becomes nonlinear, causing the generation of intermodulation products of the two drive tones. Measuring both the amplitude and phase of the intermodulation products allows one to reconstruct the nonlinearity, or the tip-surface force. Different force reconstruction methods are described in the chapter on Quantitative Analysis.
The intermodulation measurement concept can be extended to multiple drive tones and the MLA™ can be configured to drive with more than two tones. A special Drive Constructor interface is provided for setting up the multi-frequency drive and configuring the MLA™ to measure at the desired frequencies. Through a process called tuning, the MLA™ and its accompanying software force all drive frequencies to be integer multiples (or very nearly integer multiples) of one base frequency 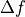 and this base frequency serves as a reference signal for lockin measurement of the response. If all the drive tones are integer multiples of the base frequency, all of their intermodulation products will also be at integer multiples of the base frequency.
and this base frequency serves as a reference signal for lockin measurement of the response. If all the drive tones are integer multiples of the base frequency, all of their intermodulation products will also be at integer multiples of the base frequency.
Such multi-frequency signals are called frequency combs because their frequency representation, when plotted as a power spectrum, looks like the teeth of a hair comb, with sharp spectral lines equally separated by the base frequency 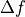 . In the time domain the frequency comb is simply a periodic waveform with period
. In the time domain the frequency comb is simply a periodic waveform with period 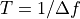 . A general statement of the intermodulation measurement concept is the following: Drive a system with a frequency comb and measure a response comb. The nonlinearity can be reconstructed from the difference between the response and drive comb. The underlying assumption is that the response is periodic on the long time scale
. A general statement of the intermodulation measurement concept is the following: Drive a system with a frequency comb and measure a response comb. The nonlinearity can be reconstructed from the difference between the response and drive comb. The underlying assumption is that the response is periodic on the long time scale 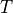 associated with the base tone.
associated with the base tone.
The MLA™ has two different modes:
Time mode¶
Time mode sends all samples to the computer, which can be a huge amount of data if the measurement time is long. Therefore, it is often favorable to down-sample the response, averaging sequential samples to give an effective lower sampling frequency. Down-sampling reduces the noise and it allows for the transfer to the computer of longer, uninterrupted streams (see Stream Recorder), but it does reduce the maximum frequency that an be analyzed. A DFT of a time mode data stream will give you the entire intermodulation spectrum, up to the Nyquist frequency, or half the sampling frequency. This spectrum reveals all the mixing in your non-linear system. When finding intermodulation products in ths manner, there is a latency between the end of the measurement time window 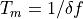 and finish of the calculation of the Fourier coefficients, which is the time require to DFT the window of sampled data. Even when using the Fast Fourier Transform (FFT) algorithm to execute the DFT, this latency is too costly when scanning over a surface. In such situations one uses the MLA™ in frequency mode.
and finish of the calculation of the Fourier coefficients, which is the time require to DFT the window of sampled data. Even when using the Fast Fourier Transform (FFT) algorithm to execute the DFT, this latency is too costly when scanning over a surface. In such situations one uses the MLA™ in frequency mode.
Frequency mode¶
Frequency mode does the Fourier Analysis of many frequencies in parallel inside the MLA™ as the samples are acquired. In frequency mode you get the full bandwidth of the MLA™ up to the Nyquist frequency set by the sampling freqeuncy of the A/D converters in the MLA. The MLA™ performs 2N Fourier sums in real-time at user-specified frequencies, where N is the number of tones in your version or the firmware. These sums give you the Fourier cosine and sine coefficients, or the in-phase and quadrature response. This response can be converted to amplitude and phase with some calculation, but often the analysis of data is more conveniently done on complex numbers.
Feedback¶
The MLA™ has a feature specifically designed for AFM, where feedback is required to track the surface when scanning. The amplitude of response at one dedicated feedback frequency is calculated inside the MLA™. This amplitude is subtracted from a set-point amplitude, forming an error signal. A voltage proportional to this error signal is sent to one of the output ports. In order to make the feedback more responsive, the MLA™ updates the error signal 250 times in the measurement time window 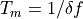 . The sections on Setup Feedback and Drive Constructor give more information on how the configure the feedback and set-point.
. The sections on Setup Feedback and Drive Constructor give more information on how the configure the feedback and set-point.
